So you've heard of Elliptic Curve Cryptography. Maybe you know it's supposed to be better than RSA. Maybe you know that all these cool new decentralized protocols use it. Maybe you've seen the landslide of acronyms that go along with it: ECC, ECDSA, ECDH, EdDSA, Ed25519, etc. Maybe you've seen some cool looking graphs but don't know how those translate to working cryptography. The articles you find online either don't answer your questions, or launch in to a 30 minute description of birational equivalence.
We feel your pain. We wanted to create a resource that answers all those questions you have, gives you a cheat sheet for those pesky acronyms, and takes you from crypto-kindergartener to elliptic-expert in less than 10 minutes.
Enough with the talk! I just need to figure out what all these funky acronyms mean!
RSA: Rivest–Shamir–Adleman (the three inventors of RSA)
Old school cryptography that uses prime-factorization
ECC: Elliptic Curve Cryptography
New-fangled cryptography that uses elliptic curves. More secure & smaller keys than RSA.
ECDH: Elliptic Curve Diffie Hellman
Key-sharing algorithm used for asymmetric encryption
ECDSA: Elliptic Curve Digital Signing Algorithm
Digital signing algorithm using elliptic curves (makes sense right?)
Edwards Curve:
A special type of elliptic curve (most are Montgomery Curves). Faster for certain operations.
EdDSA: Edwards Digital Signing Algorithm
Digital signing algorithm using an Edwards curve. Runs in constant time.
Ed25519: Edwards Curve 25519
The most commonly used Edwards Curve
Curve25519:
The non-edwards companion to Ed25519
secp256k1:
The curve used by Bitcoin & Ethereum
NIST Curves:
Curves created and standardized by the National Institute of Standards and Technology
What is asymmetric cryptography?
Asymmetric cryptography (or "public key cryptography") is a cryptographic system that uses keypairs (a private key and a public key). The public key is shared widely, while the private key must be kept
completely secret.
There are two main use cases for public key cryptography: asymmetric encryption and digital signatures.
Asymmetric encryption is a method by which Alice can send a message to Bob without leaking any information about her private key to Bob and nothing about the key or the message to the outside world.
Digital signatures are a means of verifying that a message came from the holder of a certain private key and that the information has not been tampered with in flight.
How on earth does that work?
All public key cryptography relies on the existence of one-way functions: mathematical functions that are very easy to calculate in one direction but nearly impossible to "undo", or calculate in the other direction.
RSA has been the predominant cryptosystem since its introduction in 1977. It relies on prime factorization of very large numbers.
Prime factorization is the process of breaking a number down into the product of prime numbers. This is easy with small numbers: for instance, the prime factors of 70 are 2 * 5 * 7. Now do that with a 2048-bit integer, and it ends up being pretty complicated.
Sweet good thing someone figured that out. Now we can all kick back and relax knowing all of our information is secure!
Well, computers are a lot faster nowadays than in 1977. Unfortunately that means that they're also getting faster at factoring large prime numbers. While a 256 bit key might've cut it at one point, now that key can be broken in ⌚👀, 103 seconds.
Computers and prime numbers are now in an arms race, with the current key size recommendation being 2048 bits. As keys get larger, operations obviously become slower. Meanwhile, the threat of quantum computing looms on the horizon. The now infamous Shor's algorithm threatens to solve prime factorization in polynomial time. Which would render RSA as good as done.
Is there no hope for privacy?!
There's a new one-way function on the block: Elliptic Curve Cryptography. Now with 100% less prime factorization!
What's an elliptic curve?
Elliptic curves are cool looking curves that look like this:
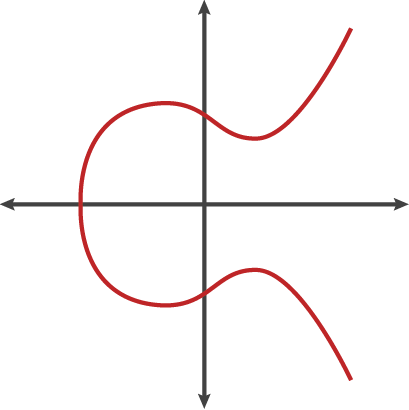
And are graphed with equations that looks like this:
y^2 = x^3 + ax + b
Except decimals are a bit unruly so we only take the integers, and then take a modulus of the function (basically wrap the graph around the edges like an old game of snake), so the graph actually ends up looking something like this (note there's still a horizontal line of symmetry):
Alright, but what do these have to do with cryptography?
The basic procedure of ECC is this:
- Choose a curve and a point
Pon the curve (everyone uses the same point) - Choose an arbitrary very large number
N(this is your private key). - Using point addition, add
Pto itselfNtimes - The x-coordinate of
N*Pis your public-key
Can you ground this in reality a bit?
Sure! Let's draw an analogy to adjusting a clock. Here are the same steps listed out but with a clock instead of an elliptic curve:
- Grab a clock sitting at exactly midnight and choose an arbitrary number of seconds
P - Choose a very large number
N - Move the clock forward
PsecondsNtimes (pretend you have really fast hands 😜) - Give the clock to a friend and tell them how big each step was (
P) then see if they can figure out how many times you moved it (N) to arrive at the current location
And how well does this whole thing work?
It turns out this is a much more robust one-way function than prime factorization. In fact, we can achieve the same security as a 3072-bit RSA key with a 256-bit ECC key. Not bad!
What if someone guesses the same number N that I chose?
There's a mind-blowingly large range of numbers to choose from. Each key is 256 bits so you have 2^256 = 10^77 options. To give you a scale of how big this is, there are:
~10^18grains of sand on earth~10^22stars in the observable universe~10^78atoms in the observable universe
So guessing someone's private key would be approximately equivalent to guessing a random atom in the universe.
Doesn't it take a long time to calculate my public key?
Nope, point addition is associative. Meaning:P + P + P + P = (P + P) + (P + P) = 2P + 2P
So when calculating a N*P for a very large N, you only need to calculate P + 2P + 4P + 8P...
At most, you must calculate 256 terms. Trivial for a computer. But to guess the public key for a given private key, you would need to check every number in between (that big number we talked about earlier).
How do these keys translate into cryptographic functions?
ECDH is a key sharing algorithm, most commonly used to send encrypted messages. ECDH works by multiplying your private key by another's public key to get a shared secret, then using that shared secret to perform symmetric encryption.
To illustrate why this works:
- Alice and Bob agree on a curve with starting point
P - Alice has a private key
aand public keyA = a * P - Bob has a private key
band public keyB = b * P a * B = a * b * P = b * A- So
a * b * Pends up being the shared secret
ECDSA is a signature algorithm, used to prove authenticity of some information. The algorithm is a bit trickier than ECDH.
Warning: lots of equations, feel free to skip to the takeways below.
- Alice and bob agree on a curve with starting point
P - Alice has a private key
aand public keyA = a * P - Alice chooses a random
kand pointK = k * P - Alice takes
rwhich is just the x-value ofK - Alice hashes her message to produce hash
H - Alice calculates a value
s = inv(k)*(H+ra) - Alice sends her message to Bob along with the signature
(r, s) - Bob calculates
Hfrom the message - Bob ensures that
r = H*inv(s)*P + r*inv(s)*A - If it does, the signature is valid!
If you skipped those equations or they don't quite click, the key takeaways are:
- Alice sends a random value
rand a calculated valuesthat could only be calculated with a combination of the private key, the message hash, and the random value, but gives away no information about her private key. - Bob can verify
randsby using just the message hash and Alice's public key - You need a good source of randomness to use ECDSA. If you're randomness function is broken, repeated signatures can disclose your private key
Real quick, you mentioned symmetric encryption. How does that work?
Symmetric encryption uses just one key to encrypt and decrypt a message. Encrypted messages just look like random jumbles of letters and numbers that give no information about the underlying message unless you have the key to "unjumble" it. Most algorithms use a block cipher. This involves choosing a block size (say 64 bits), and encrypting the message in blocks of that size.
We mentioned symmetric encryption when talking about ECDH. When people say "asymmetrically encrypted", they actually mean "symmetrically encrypted with a secret that is shared asymmetrically".
A few examples of algorithms are AES, Salsa20, or Triplesec (which is actually just a combo of the first two for extra security).
Okay, I generally understand how this works, but how do people decide on a curve and a point P?
A bunch of different ways, sometimes they're chosen for a specific reason, sometimes they're algorithmically determined. Different curves have different properties. Checkout Safe Curves for an analysis of different curves.
Can "faulty" curves give backdoors?
Yes! Faulty curves can give shortcuts to determining a private key from a given public key.
Many suspect that NIST curves have NSA backdoors in them. This is because a published NIST randomization algorithm (that the NSA tightly collaborated on) was found to have a backdoor. We encourage you not to use any curves published by the NIST!
What's this "Edwards Curve" I keep hearing about?
Most Elliptic curves are Montgomery Curves. Edwards Curves were described by mathematician Harold Edwards and popularized by cryptographer Daniel Bernstein. They have a different structure that allows for a faster signature algorithm. This signature algorithm, when performed on an Edwards curve, is called EdDSA. This algorithm runs in constant time, meaning it's faster and leaks less information
Can Edwards Curves do key sharing?
Edwards curves are specifically used for signatures. There is not a related Diffie-Hellman key sharing algorithm.
So if I want to use both ECDH & EdDSA, I need two key pairs?
Not exactly. Let's take the most common Edwards curve Ed25519. This curve is related to Montgomery curve Curve25519. In fact Ed25519 is a twist of Curve25519. A "twist" basically means that the curves are mappable to one another. What this means is that you can use the same private key to generate a public key on both curves and then transform those public keys between one another without any knowledge of the private key. Specifically, with these equations.
(u, v) = ((1+y)/(1-y), sqrt(-486664)*u/x)
(x, y) = (sqrt(-486664)*u/v, (u-1)/(u+1))
where (u, v) is the Curve25519 point and (x, y) is the Ed25519 point
You can read a more in-depth post about that Here.
What cryptography algorithms do protocols like Bitcoin, Ethereum, and IPFS use?
Bitcoin uses secp256k1 for completely arbitrary reasons
Etherem uses secp256k1 for interop with Bitcoin
IPFS uses Ed25519 and RSA.
Okay so what do you recommend?
We're using Ed25519 & Curve25519. We chose these because:
- They are well-recognized as safe curves
- They are one of the more commonly used curves, so we have easier interop
- They allow us to use EdDSA for signatures
- We're fairly certain that they don't have any backdoors in them
This is sweet! Why doesn't everyone have a private key??
We ask ourselves the same question everyday. The main reason is: it's a pain. Keys look scary (6A576D5A7134743777217A25432A462D4A614...). And if you lose a key, you're forever screwed. There's no "recovery by email" available.
What are people doing about this?
We need to fix the UX of public keys. Remove the scary hexadecimal strings and provide more painless recovery.
A few options are
- Replication: Share the same key across multiple devices. If you drop your phone in a lake, you can recover your key with your laptop
- Shamir Secret Sharing: This involves splitting a key up into separate "shares". Each share reveals nothing about the key, but by combining the shares back together, you can recover the private key. This leads to interesting solutions like social recovery or zero-knowledge key recovery which we implemented as a Proof of Concept.
- Secure Hardware Enclaves: Many phones and computers that are coming out these days have Secure Hardware Enclaves. These use both hardware and software to provide very strong security gurantees
- Hardware Secure Modules (HSMs): These are similar to Secure Hardware Enclaves, but larger and hold more information. Physical modules exist, and you can also rent space from cloud providers such as AWS. Less security-minded users might be interested in backing up their keys with a "trusted custodian" (this still ends up being quite a bit safer than the internet's current security model).
How are you using private keys?
Here at Fission, we wanted to get private keys into the hands of our users as quickly as possible. We just rolled out our new authentication scheme which uses private keys to power our command linetool: Fission Live. Give it a go and let us know what you think! We have other big projects coming down the pipeline soon that will use this public key infrastructure to power some really neat features: a global encrypted filesystem, cryptographically verifiable claims, and more!
